电动力学应该是四大力学里脉络最清晰的一门,因为所有的经典电磁现象无非就是麦克斯韦方程的解,在不同的情况我们使用麦克斯韦方程不同的写法,这里写四种。方程的物理意义普物电磁学已经谈过,这里不再讨论。
(一) 积分形式麦克斯韦方程
积分形式的麦克斯韦方程为:
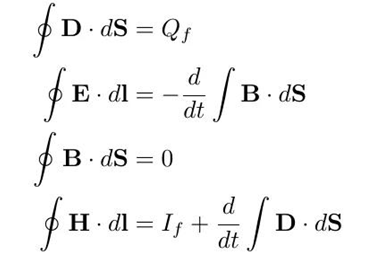
众所周知,积分某种程度上就是一种求和或者取平均的操作(积分中值定理),积分形式麦克斯韦方程就是用在这种需要平均的地方,也就是当电荷分布或者自由电流分布在界面上出现不连续的情况时。什么时候界面会出现电流电荷分布的不连续?也就是不同介质的交界面上。

在一个界面上如果存在不连续的电荷分布,首先造成电场法向分量不连续:
取一个薄高斯面包围界面一点,根据第一个麦克斯韦方程,得到不连续的值为:
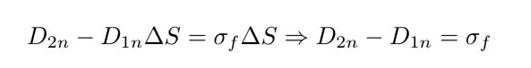
再做一个环路包围界面一点,穿过两种介质,可以得到电场切向分量是连续的。
对磁场如法炮制,得到法向分量是连续的(第三式),切向分量是不连续的(第四式):
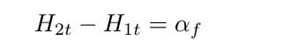
统一以下,写成矢量形式就是:
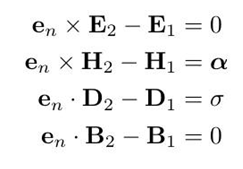
(二) 微分形式麦克斯韦方程
根据高斯定理和斯托克斯定理,我们可以立刻把积分形式麦克斯韦方程写成微分形式:
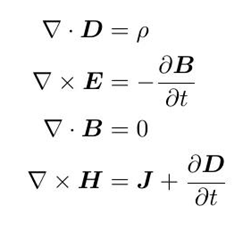
微分形式麦克斯韦方程+积分形式得到的边界条件,可以解决大多数问题了,当电磁场不含时的时候,我们要解决的就是静电静磁问题:
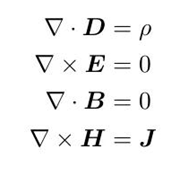
2.1 静电场
注意到静电场旋度是0,因此它是保守场,因为标量梯度的旋度总是0,所以存在标势Φ,满足:
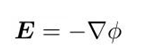
解决静电学的方法有很多种,但无非都是叠加原理思想的运用。
第一种是直接用库伦定律+叠加原理。库仑定律告诉我们,一个点电荷激发的电势为:
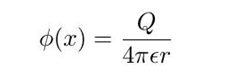
对于一个给定了电荷分布的系统,使用叠加原理
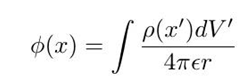
第二种是解泊松方程,在线性,各项同性的,均匀的介质中,电位移矢量D和场强E只差一个介电常数ε:
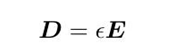
把标势代入电场散度中,得到泊松方程:
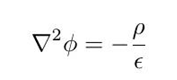
在没有电荷分布的地方,标势也就满足拉普拉斯方程:
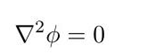
求解的方法很多,参见数学物理方法。叠加原理得到的Φ就是泊松方程的一个特解。
第三种是对特解进行多级展开,因为特解的积分不好求,因此把它展开成泰勒级数,因为各阶的系数(电多级矩)是好求的,只要我们展开够多,得到的结果就更精确:
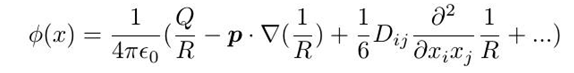
2.2 静磁场
磁场旋度一般不是0,因此不是保守场,但它的散度是0,因为矢量旋度的散度总是0,因此我们可以定义失势:
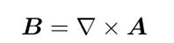
于是多了一个静电场不存在的麻烦:我们完全确定一个场,需要知道它的旋度,散度和边界条件,静磁场中引入了新的场A,并且知道了A的旋度,但我们不知道它的散度,也就是说引入矢势后增加了一个方程,如果需要唯一解,我们需要为A添加新的约束条件,不同约束条件就是所谓不同的规范。静磁场中我们选取库伦规范为约束条件:
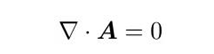
在非铁磁性介质中,H和B也是线性关系:
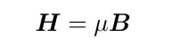
对磁场两边取旋度,得到:
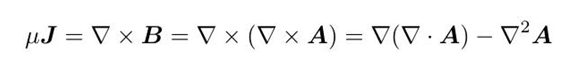
在库伦规范下,失势A满足泊松方程,于是回到了静电学求解的套路,我们可以对A再来一遍。
(三) 洛伦兹规范下的麦克斯韦方程
对于微分形式麦克斯韦方程(真空为例):
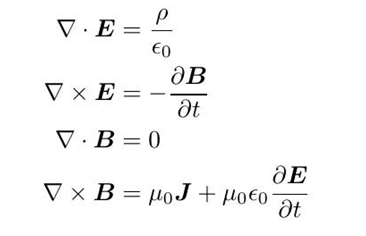
因为B散度总是0,因此失势在非静磁情况同样可以接着用:
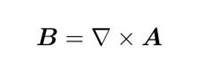
但电场已经不保守了,接下来要重新构造标势(找旋度为0的场)
把矢势代入方程第二式
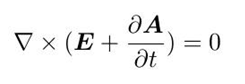
注意到一对势A和Φ对应了B和E,但这对势不是唯一的,经过规范变换,我们可以找到另外的对应相同B和E的势:
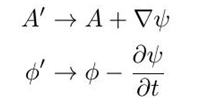
现在把势代回麦克斯韦方程,得到:
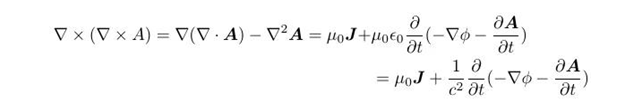
整理一下:
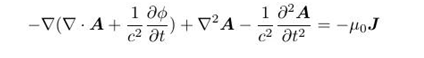
现在我们取洛伦兹规范:
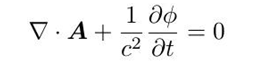
就得到了达朗贝尔方程:
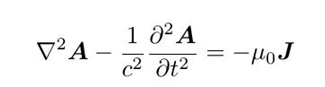
同样的,使用洛伦兹规范可以得到标势也满足达朗贝尔方程:
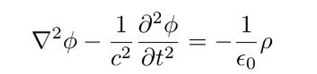
所以电磁场以波的形式传播,波动方程的解是推迟势(比静电势推迟了一点时间):
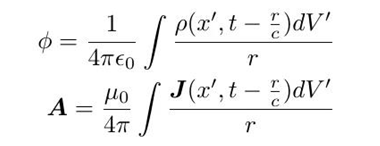
也就是说,电磁相互作用是有传播速度的,即光速:
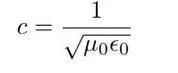
特别的,在自由空间里,特解就是平面波:
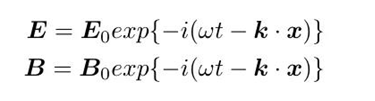
把平面波的解代入界面边界条件,即可得到反射定律,折射定律,由能量守恒就能得到菲涅尔公式。
考虑电磁波辐射的时候,辐射源的势进行多级展开,就可以得到电偶极,电四极,磁偶极等贡献的辐射,其中电偶极辐射占主要,磁偶极和电四极的贡献在同一个数量级,比电偶极小几个数量级。
(四)张量形式的麦克斯韦方程
以下的我们会用张量的记号处理问题,详情参见 张量分析初步。
狭义相对论中,不同惯性系之间的坐标变换称为洛伦兹变换,洛伦兹变换有两个基本假设:
1.光速不变
2.所有惯性系中,物理规律有相同的表达形式
洛伦兹变换中,时空被耦合在一起,因此相对论的时空是四维的,第四维度是时间,为了对其量纲,我们让时间乘一个光速。定义协变矢量:
逆变矢量:
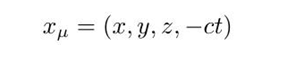
根据光速不变,我们能得到第一个洛伦兹不变量:时空间隔(注意求和约定)
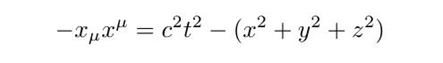
郭硕鸿版教材把协变矢量和逆变矢量统一了,第四维度用乘了个i,这样数学形式不好看,所以这里使用张量统一的形式。
根据假设2,我们可以得到洛伦兹变换是线性变换,根据假设一推出的时空间隔不变,我们得到线性变换的矩阵:
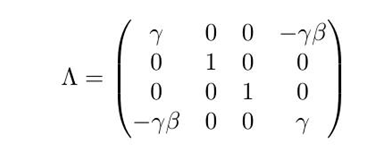
其中:
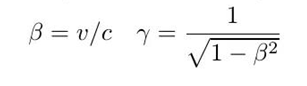
四维线性变换的形式为:
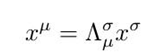
容易得到动尺收缩(同时不通地)和时间膨胀(同地不通时)效应:
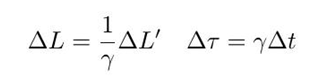
在狭义相对论中,电动力学是具有洛伦兹不变性的,在洛伦兹规范下,标势和失势满足达朗贝尔方程:
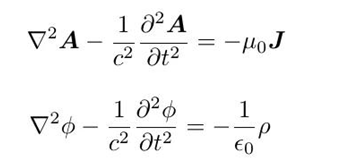
事实上,达朗贝尔算符就是四维下的laplacian:
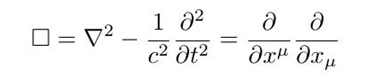
如果把势和电流密度写成四维形式:
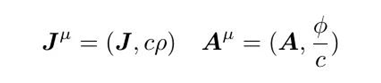
就可以把两个方程和为一个:
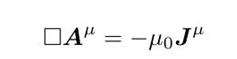
并且洛伦兹规范也可以写成简洁的形式:
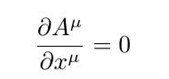
再进一步,我们凑出电磁场的拉格朗日量密度,把它写成最小作用量原理的形式(拉格朗日方程),只需构造四维张量:
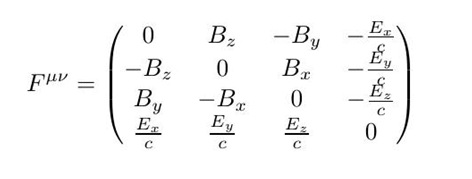
拉格朗日量是标量,所以我们要把张量变成标量形式,最简单的操作莫过于:
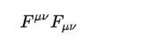
电磁场的拉格朗日量密度就出来了:
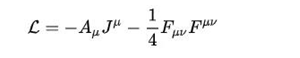
代入拉格朗日方程,我们得到麦克斯韦方程的第一个和第四个(其实是麦克斯韦方程凑拉格朗日):
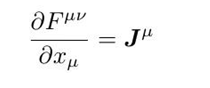
第二个和第三个则满足:
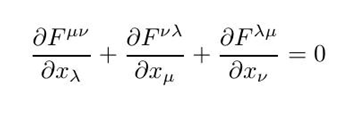
当然,注意这个张量的上标,它是协变的:
(1)、麦克斯韦方程组的适用范围及其物理意义
(2)、麦克斯韦方程组积分形式及其意义
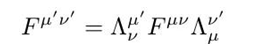
这也是电磁场的变换关系。
















